Expected smoothness for stochastic variance-reduced methods and sketch-and-project methods for structured linear systems (PhD thesis)

Abstract

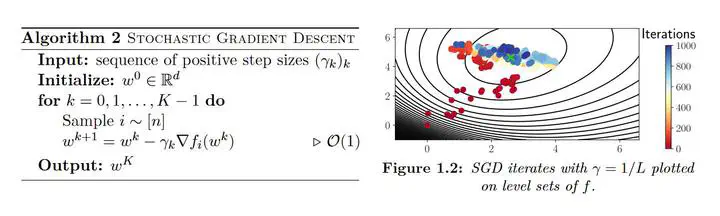
The considerable increase in the number of data and features complicates the learning phase requiring the minimization of a loss function. Stochastic gradient descent (SGD) and variance reduction variants (SAGA, SVRG, MISO) are widely used to solve this problem. In practice, these methods are accelerated by computing these stochastic gradients on a “mini-batch”: a small group of samples randomly drawn.Indeed, recent technological improvements allowing the parallelization of these calculations have generalized the use of mini-batches.In this thesis, we are interested in the study of variants of stochastic gradient algorithms with reduced variance by trying to find the optimal hyperparameters: step and mini-batch size. Our study allows us to give convergence results interpolating between stochastic methods drawing a single sample per iteration and the so-called “full-batch” gradient descent using all samples at each iteration. Our analysis is based on the expected smoothness constant which allows to capture the regularity of the random function whose gradient is calculated.We study another class of optimization algorithms: the “sketch-and-project” methods. These methods can also be applied as soon as the learning problem boils down to solving a linear system. This is the case of ridge regression. We analyze here variants of this method that use different strategies of momentum and acceleration. These methods also depend on the sketching strategy used to compress the information of the system to be solved at each iteration. Finally, we show that these methods can also be extended to numerical analysis problems. Indeed, the extension of sketch-and-project methods to Alternating-Direction Implicit (ADI) methods allows to apply them to large-scale problems, when the so-called “direct” solvers are too slow.

Nidham Gazagnadou

Research Scientist

My research interests include federated learning, edge AI and computer vision privacy.